One of my favorite things about electronic dance music is how tirelessly and mindlessly popular synth sounds are exploited. It’s awesome! One of the big sounds of the turn of the millennium was the so-called supersaw, an extremely bright, cold, digital, huge lead sound. You rarely hear it now in non-ironic music, but anyone who was listening to anything dancey and stupid around 2003 will surely recognize it.
Here’s a fairly typical example:
Other big choons that have similar leads are “Ramp” by Scooter, and “Heaven” by DJ Sammy.
The canonical synth for producing this kind of sound is the Roland JP-8000 (or the rack-mount JP-8080), released in the mid 90s. As the sound became trendy in dance music, the ability to produce these obnoxious, blindingly bright monstrosities quickly became a bullet-point feature for competing synths – Novation’s Supernova 2, and the later Virus TI had similar features.
So, what is the supersaw? According to roland’s marketing material, it “sounds like seven saw waves sounding simultaneously”.
Okay, fine. But what is it really? It’s important to remember this was the mid-90s, processing power was tight, and running 7 saws for each note sounds pretty expensive. There must have been some trickery at play.
I always think it’s awesome when products of economical engineering remain relevant long after their shortcuts are no longer needed. This seems to happen a lot with music equipment, and Roland had a pretty good run of devices in this category – the TB-303, D-50 and the Juno series all remained popular long after the constraints they were designed for no longer applied. Once you get into the digital era, these stories of engineering ingenuity get harder to tell. With discrete circuitry, you can just look at the circuit to see what choices the designers made, and how those choices create the sound you hear. With software, all you really have to go on is the output of the device – which can sometimes be a bit inscrutable.
I had sort of resigned myself to never knowing how wonders like the supersaw were produced, until I stumbled upon this awesome thread on KVR. It turns out there are some tell-tale signs that give pretty strong indications of how the supersaws were produced – and the engineering is just as goofy, simplistic, and beautiful as I had hoped, and I’ll spend the rest of this post reviewing the results from that discussion, and re-creating a JP-style oscillator in pure data.
The fundamental problem of digital oscillator design, at least for simulating analog waveforms, is aliasing. Directly synthesizing a saw wave produces harsh noise all over the spectrum. There are lots of ways of getting around this – wavetables and oversampling are probably the most popular commercially, but academia has given us other options too. A lot of hobby programmers use something called BLEP. Korg recently patented a variant of BLEP, too.
Of course, another path is to do nothing to the aliasing and embrace its roughness for what it is. There’s good reason to believe that’s exactly what Roland did in the supersaw.
First, for reference, here’s a nice, modern, anti-aliased (bandlimited) saw wave at 130hz, generated by the free TAL Noisemaker.
As you can see in the spectrogram above, there’s defined peaks at each harmonic and not much noise in between.
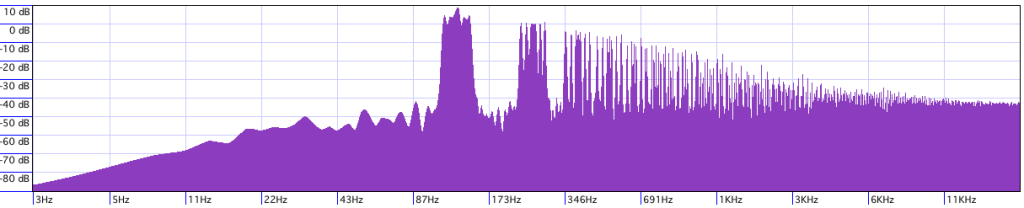
Let’s see what a totally aliased, digital-as-hell saw sounds like. We easily use puredata’s phasor~ to make a aliased saw:
You can hear it’s a bit more nasally and unpleasant. It doesn’t sound too different because the frequency of the note is relatively low – the aliased harmonics aren’t very loud. In the spectrum above, you’ll see more differences: the harmonics are still there, there’s lots of aliasing noise between them.
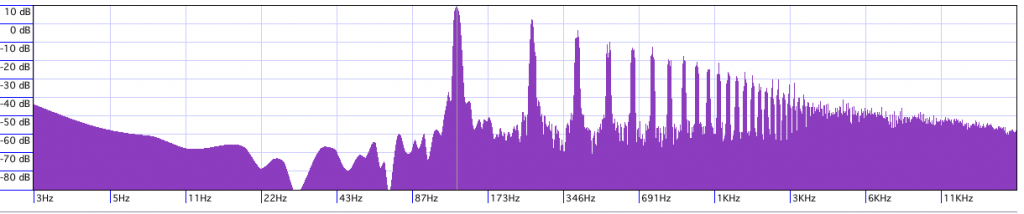
If you turn down the “mix” slider for the supersaw, it becomes a simple saw wave – but with some interesting properties. Here’s the JP-8000’s attempt at a non-super saw at 130 hz.
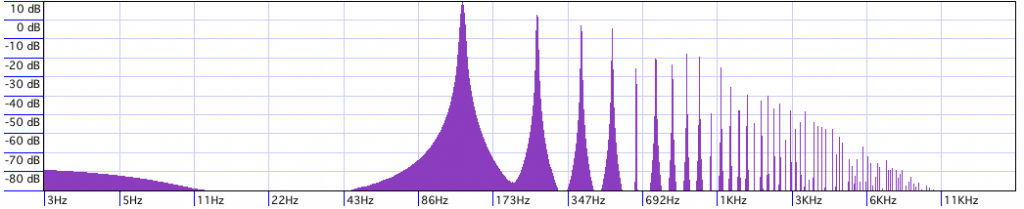
As you can see and hear, it’s closer to the aliased saw wave from than the saw from band-limited synthesis. There is a notable difference, though, pointed out by the folks at KVR – the noise *below* the first harmonic is significantly less. To make this more clear, here’s the PD aliased saw at 520 Hz:
And the JP at a similar frequency:
Now the low-frequency noise is quite different between the two. It seems that the JP generates an aliased saw and then runs it through a high-pass filter set to only pass frequencies at or above the fundamental of the note. This leaves in all the aliasing noise above the fundamental, so it’s still pretty nasty/noisey sounding, but there’s no energy below the frequency of the note to distract you from the pitch.
Let’s try to approximate that with PD:
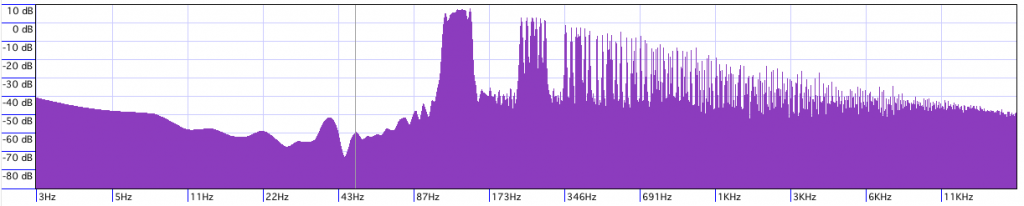
Clearly not exactly the same as the filtering scheme is different (the JP seems more like a biquad hi-shelf), but it’s still not a bad likeness.
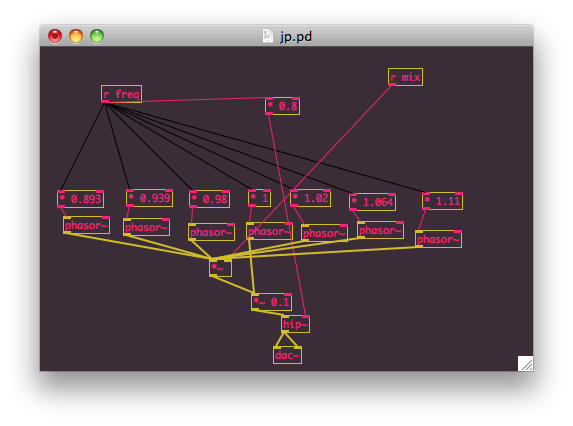
Now let’s try to reverse-engineer the spread of the saws – originally in the KVR thread people were suggesting complicated schemes based on a chorus effect, but it seems clear from the spectrum of a fully detuned supersaw wave that no, the JP really is generating 7 saw waves:
This makes sense when you think about it – efficiency was king, and it’s hard to beat the efficiency of two extra adds per sample – things are a lot easier when you embrace aliasing rather than reject it, huh?
Int the spectrogram above, we can see that there are indeed 7 peaks at each harmonic – indicating that there are 7 saw waves. Each peak is pretty well defined, indicating that there’s not a lot of low-frequency vibrato going on.
The third harmonic seems like the easiest to pick out the peaks, we’ve got:
(rounded to whole numbers):
350, 368, 384, 392, 400, 417, 435.
So, the detuning ratios are then
(.893, .939, .980, 1.0, 1.020, 1.064, 1.110), or slightly assymetrical.
Again, let’s try this in PD.
Not entirely dissimilar, huh? To be fair, a lot of detuned waveforms have a spectrum that kinda looks like that. But if I use my ears I can definitely hear some similarities.
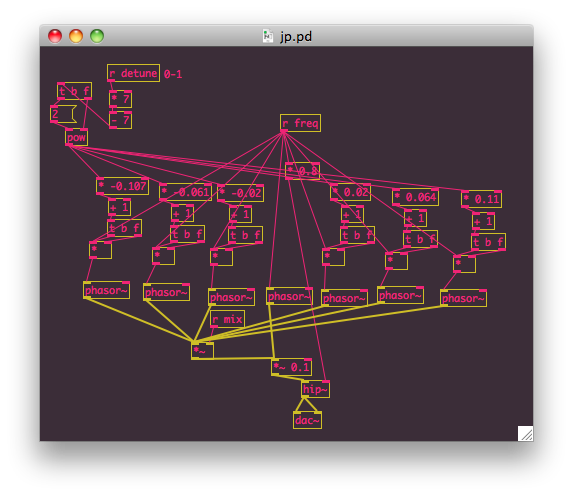
Now that we have no-detune and max detune in the bag, lets look at what happens at other detune settings. At 0% detune on the slider, there’s still a little bit of audible detune, but not quite enough to see it on the spectrum. We can’t see anything on the spectrum until about 3/4 of the way on the slider, which has a spread of around 15hz at the harmonic at 520 hz:
That means the total spread is around 0.987 – 1.013 rather than the full value of 0.893 – 1.110. This dramatic increase in detune at the end of the sweep of the slider implies there’s some sort of exponential scaling occuring.
To simulate this in PD, I’m just making a guess about the endpoints of the detuning and the fact that it uses log2 scaling.
Sounds pretty good! This PD patch definitely captures the major character points of the JP supersaw oscillator. Here’s some sweeps of the detune knob:
Hands Up!







“This makes sense when you think about it – efficiency was king, and it’s hard to beat the efficiency of two extra adds per sample – things are a lot easier when you embrace aliasing rather than reject it, huh?”
I don’t get it–two extra adds to do what? Or do you mean the 7 sawtooths really are just 7 sawtooths?! Thats the secret?! And if so why only for sawtooths?
One way of implementing a sawtooth wave is to start from zero, then, each sample add 1/period to it, and then when it reaches one, wrap around to zero. So, if you want a sawtooth wave with a period of 10 samples, it would start at 0, then become 0.1, then 0.2, etc. This is exactly what the “phasor~” does in the demos and it’s often called a “naïve saw wave”.
This works fine for waves with periods of integer number of samples, but sounds really noisy for non-integer periods, say 10.1 samples. This noisyness is called “aliasing”, and there are several places online that try to explain how it comes about. Aliasing is still one of the biggest issues in digital synthesis, because in music at common sample rates, most pitches we are interested in have non-integer periods.
Okay, but if you don’t care about aliasing noise (and apparently Roland didn’t), you can use the plan I devised in the first paragraph. To create another saw wave in your mix you require two more “addition operations” per sample – one to increment the saw to its next value, and another to add the saw wave to the output mix. Of course, you also have to check if the saw has gone past 1. But still, this is more efficient than most “alias-free” saw wave algorithms, which was my only point.
I’m not sure about other waveforms – I actually don’t have a JP-8000 at home that I can use to do an analysis of them. The supersaw is the most unique of the JP-8000’s oscillators, and it’s an iconic sound in dance music. That’s why the blog post focused just on the supersaw wave.
I’m pretty interested in alias-free saw waveforms (yes, yes, this is embarassing), and the literature on the subject is a bit confusing , so I may do a series of blog posts on them in the future.
Depending on the CPU architecture, you might not. If you’re computing in 16-bit signed integer, for example, you just increment by freq * 2^16 / samplerate and let the natural integer wraparound take care of it, or given that you’re going to be summing 7 of them, you probably need to mask out 2-3 high bits before the accumulation.
Good point. Indeed, it’s pretty likely that roland used this technique.
.893, .939, .980, 1.0, 1.020, 1.064, 1.110 …
Are you sure? The sidebands are actually 2 SEMITONES away from the carrier? Sure you don’t just mean like 2, 6.4, and 11 CENTS?
Yup! It’s pretty gnarly. Keep in mind, that’s the absolute maximum of the detune slider, and there’s some sort of exponential scaling on the slider such that it becomes more tame pretty quickly. 3/4 of the way up the slider the detune spread is only 22 cents.
Very interesting post right there. Actually I tried to build myself a very basic additive synth to try building a supersaw. The only thing it does is taking 7 saw waves and add them together. As simple as that…
I successfully managed to detune the waves in a way that matches very well the JP8000 spectrum.
But now I have a huge problem. My synth suffers from extreme feedback issues. Basically the 7 saws are overlapping at regular intervals. This is VERY annoying, but also somewhat expected, since when the waves have a similar frequency they tend to produce feedback naturally, yes?
What bugs me is that you managed to avoid feedback almost completely. How did you do that?
You shall check out a sample and see for yourself:
http://www.mediafire.com/?yht56f42f6hluvu
You can compare it against the fully detuned JP sample from your article.
Any help. Thanks.
It sounds like you are talking about beating, which occurs whenever you have two or more detuned waves. Depending on the frequency difference between the oscillators, beating can be be perceived as richness, dissonance, or tremolo. There are no totally solid rules for how to avoid the tremolo sound, but one approach that seems to work is to use complicated ratios between oscillator frequencies, rather than evenly spacing them. This will make the least common multiple of the frequencies quite large, which means a longer time before the sound repeats. Did you try the frequency ratios given in this article? They should work quite well.
> It’s important to remember this was the mid-90s, processing power was tight, and running 7 saws for each note sounds pretty expensive. There must have been some trickery at play.
Exactly… But, instead of investigating a possible trick, you did follow the additive way, adding 7 detuned OSC.
I’ve been lucky to work and discuss with the designer of the JP-8000. Being close to the engineer team at that time, I’ve been told the secret (under NDA) . Pure genius. You are totally right, at that time, CPU power was too tight. So, they found something clever, so clever. Very creative engineering. Kudos to Roland engineers.
Well, I guess the quest for trance authenticity continues for the rest of us, then. At the very least, the additive saw wave approach mentioned in this article is incredibly computationally cheap and is passable to my ears. I was working from samples rather than a real unit when I wrote this – maybe someday I’ll get a unit and do a more thorough analysis.
did you have a need to know the secret or did your friend break his own NDA?
i mean you could have told us the secret if you didn’t include such a rich back story.
i’ll go with “wavetable”
Nice writeup,
Any thoughts on how the feedback oscillator works?
mtm
Interestingly, the Virus TI offers a HyperSaw effect on any oscillator (wavetable!) shape. Do you think they do that naively by adding 7 oscillators? I suspect that would cost them too much CPU, especially with the interpolation required by the wave-tables, so they must have some other trick up their sleeve. Note that turning on HyperSaw on the Virus does reduce polyphony but not by a factor of 7.
Really interesting question. The TI is a fairly powerful machine compared to the JP, so it might actually be really doing 7 oscillators. The TI runs filters, envelopes, and amps per voice in addition to the oscs, so switching to 7 oscillators wouldn’t necessarily take up the same CPU as 7 voices.
Every analysis of the supersaw always seems to jump to the same conclusion: as there are, in fact, seven saws, Roland must have actually implemented seven saw oscillators. I don’t know what they did, but my best guess (so far) is below.
I haven’t analyzed the supersaw oscillator myself, but based on the numbers presented here, the side oscillators ARE, in fact, symmetrically around the center oscillator (within given precision), just not on logarithmic, but linear scale. This should tell us something.
You can generate two saw waves with a phase shift out of one by sending it to a comparator and summing the output with the original saw waveform. The generated pulse wave should be scaled to half the amplitude of the saw wave. The other comparator input controls the phase shift, so if we drive it with a saw wave LFO, we get two saw waves, the original and one whose frequency differs from the original by the frequency of the LFO. Whether the generated second saw wave has higher or lower pitch than the original depends on the net polarity of everything, but in an otherwise identical arrangement, reversing the polarity of the LFO generates the second saw wave on the opposite side of the original pitch. Thus, with a single LFO and two comparators, we can generate three detuned saw waves out of one.
This may initially seem like something that is more economical in an analog synthesizer than in a digital one. However, in ordinary binary arithmetic that wraps around on overflow, a comparator whose output is mixed with the input is equivalent to an addition. Thus, we can write our three oscillators as
out = ((osc + lfo) >> 1) + ((osc – lfo) >> 1);
where osc is the center saw wave and lfo is the detuning LFO. Something like supersaw would then be
out = S * (((osc + lfo1) >> 3) + ((osc – lfo1) >> 3) + ((osc + lfo2) >> 3) + ((osc – lfo2) >> 3) + ((osc + lfo3) >> 3) + ((osc – lfo3) >> 3)) + C * osc;
where weights S and C are used to control the amplitude relationship between the center and the side oscillators.
As you pointed out, it’s hard to beat the efficiency of two additions per additional oscillator, and, in fact, the code above not only adds the two additions, but the cost of calculating the LFOs as well. However, oscillators require much higher precision (for tuning) than the trickery described above; with a little bit of adjustment, the final waveform could probably be calculated using just eight bits (which would suit the SNR of the JP-8k). As we only need to calculate four saw oscillators instead of seven, and out of those only one needs to be updated for every sample, it is likely possible to make this faster than the trivial solution.
Disclaimer: I didn’t try this, nor spend a lot of time thinking this through, so if I made an error somewhere, or if my method just simply doesn’t work, please forgive me.
Thanks for this. It didn’t quite work as described, but the basic concept is sound.
You only need a single LFO and a single ramp OSC (you can actually get away with just the OSC, but that makes it difficult to avoid artefacts when modulating/changing the detune amount).
Here’s a basic description of what I’ve tried, based on your suggestion of using ramp oscillators that wrap on overflow with binary arithmetic. I have implemented this in Reaktor, and it works well, although I don’t have Roland hardware to compare with, so I’m not claiming this is what they did 🙂
——————————————————————–
OSC, LFO2 //the actual ramp oscillators. LFO updating at 1/128th of audio rate
//frequency of LFO is arrived at by dividing down (right shifts) the osc frequency and multiplying by the detune factor.
lfo1 = LFO2 * 8 //bitwise rotate left by 3 should work here, or some adds
lfo3 = lfo1 – LFO2
lfo4 = lfo1 + LFO2 + offset //using a suitable offset seems to reduce beating effect a bit.
Now the 6 side oscillators can be derived
I arrived at these combinations through trial and error. I suppose some analysis with the original hardware could find more authentic combinations assuming they used this approach…
o1 = OSC + lfo3
o2 = o1 + LFO1
o3 = o2 + lfo4
o4 = OSC – lfo4
o5 = o4 – LFO1
o6 = o5 – lfo3
All that’s left is to mix these all together with OSC in whatever arrangement suits and add a high pass filter to remove aliasing artefacts below the fundamental.
How do I solve phase cancellation once I want to get back to no detune?
I’ve tried banging the phase of all the phasors every time the knob is turned but that makes horrible clicks.
I’m not sure how the original hardware did it. One option would be to smoothly align the phases over the course of a few periods.
I don’t know if this will translate well here, but I’ve stumbled on something on the Kurzweil PC3 that comes reasonably close. It looks like this:
\
—-[PWMOD]—-\
[xGAIN]—[SAW+]—[SHAPER]—
Sine (keymap)—-/
Essentially, I’m using a sine wave to modulate a DC signal via AM, which then is mixed with a sawtooth wave going into a wave shaper that, with a sawtooth as input, outputs a sine wave. I’d have thought that modulating a DC signal with a sine wave would result in… A sine wave. But I don’t get anywhere near the same result if I run a sine wave straight through (in fact on the PC3 the Sine –> SAW+ –> SHAPER results essentially in 2 op FM). Anyways, here’s a sound example of this set-up:
https://soundcloud.com/poserp/third-trance-from-the-sun
The “naked” supersaw (here run through a Chorus effect) is at the beginning. After that is what a sound nerd might do with a supersaw and call it “trance”, as opposed to what we now know as “trance”…